Luogu7715 Shape
题面
简化题意
给定一个 的 01 矩阵,求有几个由 组成的 H 形。
。
题解
首先考虑是否可以枚举 H 的竖线(每个 H 有两个竖线,这里考虑左侧)。考场上糊了一个想法:记录每一条竖着的白线,以及每一个点往右可以到达的最近的点,图示情况可以后续推乘法原理加法原理的式子做到 。随后很快发现了不可行,因为即使我记录了每一个点向右最多可以到达哪些点,整体判断一个 H 的两条竖线是否一一对应还是 的。
除此之外,即使两个 竖线部分是包含关系,也不一定代表横线部分重合,例如:


这两种情况都无法简单地区分,例如左侧这种,高度为 的 H 和高度为 的 H 竖线部分共线但是横线部分不共线。右侧这种情况说明不能只记录每一个白格子右侧第一个白格子,因为两个 H 可能只有一个竖线共线。
因此考虑竖线的情况比较难处理,又因为 H 里面只有一条横线,来考虑横线的情况。
对于任何一个 H,显然横线的两端刚好是竖线的中点。因此选择一个横线的两个端点,向上和向下延伸同样的高度(且都是白格子),就一定可以得出一个 H。
基于这种思想我们记录每一个格子向上最多可以延伸多少个格子,向下最多可以延伸多少个格子。
而显然一个横线两端的点向上和向下延伸的白格子应该是相同的,因此对于某一个格子而言,向上延伸和向下延伸的格子数取最小值,才会是以它为横线的一个端点,可能形成的高度最大的 H 的高度的一半(也就是 H 的最大高度为 )。
1 | // a 数组为输入的 0-1 矩阵 |
通过放在最前面的第一张图,我们知道同一个横线上可能出现多个大小不同的 H。假设每个横线上有若干白格子。我们发现……
(注:下图的白格子高度指的是最底下一行的横线的 )
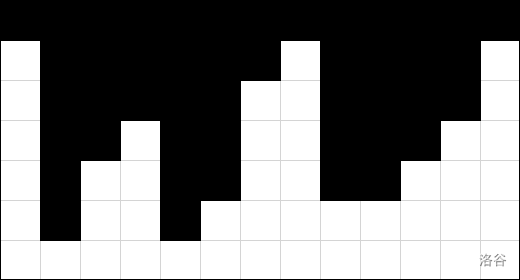
第 个可以和第 个匹配出一个 H,第 个可以和第 个匹配成一个 H……
发现高度小的一定可以和高度大于等于它的匹配。且按照这种方法匹配得出的 H 不重不漏。
因此可以每次取出一段白色的横线(设长度为 ),取出横线上每个点的 值,如果我们从小到大排个序,就会发现第 个一定可以和第 个匹配,一共有 个 H。
每一段白色的横线取出并逐个计算,累加答案。由于有一个排序,最多有 个长度为 的横线,因此总的复杂度为 的,可过。且只要有黑色的格子这东西就不会卡满。因此效率是非常可观的。
主要处理的部分:
1 | int i=1;j=1; |
- 标题: Luogu7715 Shape
- 作者: Arahc
- 创建于 : 2021-07-12 08:00:00
- 更新于 : 2023-03-19 12:05:42
- 链接: https://arahc.github.io/2021/07/12/【题解】Luogu7715-Shape/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。