CF1667F Yin Yang

Arahc 11.0
  2022-06-25 08:00 2022-06-25 08:00 创建   2023-03-15 02:54:32 2023-03-15 02:54:32 更新      1.8k 字  9 分钟  

题面

简化题意

给定一个 4n×4m4n\times 4m 的方格图，每个格子都是黑色或白色。有些格子已经被涂色了，你要给剩下的格子涂色，使得黑色格子和白色格子分别组成连通块。构造一种方案或判断无解。

保证已经被涂色的格子没有公共点或公共边。

4≤4n,4m≤5004\leq 4n,4m\leq 500，多组数据，数据组数 ≤4000\leq4000，∑nm≤250000\sum nm \leq 250000。

题解

注：题解配图中为了区分未染色格子和已染色格子，将黑白染色改为红蓝染色。

先来考虑一个简单的问题，如果四个边界上没有格子被染色，如何构造？

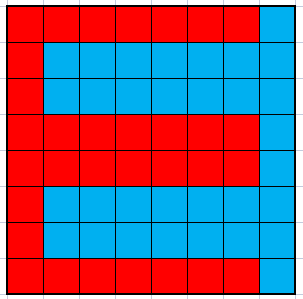
联想 AGC004C And Gird，考虑构造“梳子”状的图案，如图 1：

pic-1

考虑到任意两个限制颜色的格子不八联通，这种方案一定是可行的。

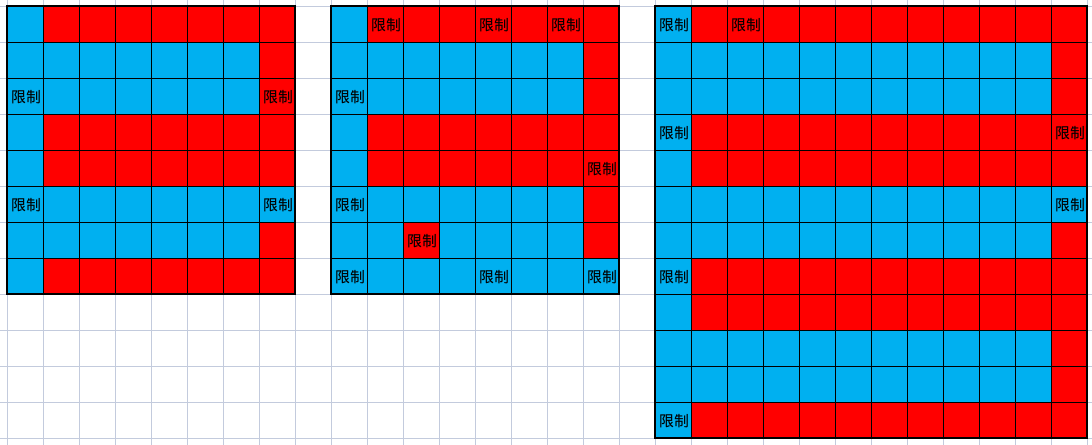
然后考虑如果边界上有限制颜色的格子怎么做。首先如果边界上存在形如 BWBW 的序列，是一定无解的，如图 2（格子上有“限制”二字表示这个格子颜色固定）：

pic-2

对于不存在形如 BWBW 序列的情况，不难发现，我们一定可以找到完整的一个边界（上/下/左/右），这条边上可以全部赋成同一个颜色，而且它对面那条边界上至少有一个点是不同的颜色。不妨把这个完整的边界上的颜色当成蓝色，参考图 1 “梳子”型构造的蓝色部分，给它安排好。

这样至少可以保证蓝色的格子相互之间可以连通了。现在处理红色格子，可以列举出如下三个不合法的情况，我们一一解决：

  1. 边框被蓝色包围了，部分边框上的红色与梳子的条纹不联通。
  2. 接近边框位置（第 22 和第 n−1n-1 行）的格子不联通。
  3. 红色梳子条纹不联通。

图 3 的三个例子分别对应了上面的三种不合法情况：

pic-3

你问我这些例子都是怎么来的？WA on test 1,2,3,17。

实际上这三种情况都可以通过简单的调整实现：

  1. 你把下面也变成蓝色不行吗？
  2. 因为上/下部分的蓝色是连通的，直接把道路打通就可以了。
  3. 显然把蓝色都连起来之后，打穿一个蓝色条纹就可以连接起来。

注意这三种调整的顺序。

（请时刻注意 BWBW 的情况早就被判掉了，在这里是不存在的。）

主要的问题是这三个，其实还有很多琐碎的细节需要考虑。个人感觉就只凭这个细节难度都能值这个 3500 了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
#include<bits/stdc++.h>
#define int long long
using namespace std;
bool Begin;
const int max_n=502;
inline int read(){
    int x=0;bool w=0;char c=getchar();
    while(c<'0' || c>'9') w|=c=='-',c=getchar();
    while(c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
    return w?-x:x;
}
inline void write(int x){
    putchar(x==2?'B':'W');
}
inline int reads(){
    char c=getchar();
    while(c!='B' && c!='W' && c!='.') c=getchar();
    if(c=='B') return 2;
    if(c=='W') return 3;
    return 0;
}

int n,m,cntr;
int a[max_n][max_n],ans[max_n][max_n];

int Tmp[max_n][max_n];
inline void rotate(){
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            Tmp[i][j]=a[i][j];
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            a[j][n-i+1]=Tmp[i][j];
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            Tmp[i][j]=ans[i][j];
    for(register int i=1;i<=n;++i)
        for(register int j=1;j<=m;++j)
            ans[j][n-i+1]=Tmp[i][j];
    swap(n,m),++cntr;
}
inline void clear(){
    cntr=0;
    for(register int i=0;i<=n;++i)
        for(register int j=0;j<=m;++j)
            a[i][j]=ans[i][j]=a[j][i]=ans[j][i]=0;
}

inline int calc(){
    int res=0;
    for(register int p=1;p<=2;++p){
        for(register int i=2;i<=m;++i)
            if(!ans[1][i])
                ans[1][i]=ans[1][i-1];
        for(register int i=2;i<=n;++i)
            if(!ans[i][m])
                ans[i][m]=ans[i-1][m];
        for(register int i=m-1;i;--i)
            if(!ans[n][i])
                ans[n][i]=ans[n][i+1];
        for(register int i=n-1;i;--i)
            if(!ans[i][1])
                ans[i][1]=ans[i+1][1];
        if(!ans[1][1])
            ans[1][1]=2;
    }
    for(register int i=2;i<=m;++i)
        if(ans[1][i]!=ans[1][i-1])
            ++res;
    for(register int i=2;i<=n;++i)
        if(ans[i][m]!=ans[i-1][m])
            ++res;
    for(register int i=m-1;i;--i)
        if(ans[n][i]!=ans[n][i+1])
            ++res;
    for(register int i=n-1;i;--i)
        if(ans[i][1]!=ans[i+1][1])
            ++res;
    return res;
}

inline bool Nice(){
    bool ok=0;
    for(register int i=1;i<=n;++i){
        if(ans[i][1]!=ans[1][1])
            return 0;
        if(i>1 && i<n && ans[i][m]!=ans[1][1])
            ok=1;
    }
    return ok;
}

int Red,Blue;

inline void findroad(int x,int y){
    if(ans[x-1][y]==Red || ans[x+1][y]==Red || ans[x][y+1]==Red) return;
    int X1=(x==2?1:n);
    if(y<=m-2 && ans[X1][y+2]==Red){
        ans[X1][y]=ans[X1][y+1]=Red;
        return;
    }
    int X2=(x==2?2:n-1);
    if(y<=m-2 && ans[X2][y+2]==Red){
        ans[X2][y+1]=Red;
        return;
    }
    int X3=(x==2?3:n-2),X4=(x==2?4:n-3);
    if(a[X4][y]!=Blue){
        ans[X3][y]=Red;
        return;
    }
    int Y=(y<=m-2?y+1:y-1);
    ans[X2][Y]=ans[X3][Y]=Red;
}

inline void bigroad(int x){
    for(register int j=2;j<=4;++j){
        bool ok=1;
        for(register int i=x-1;i<=x+2;++i)
            if(a[i][j]==Blue){
                ok=0;
                break;
            }
        if(ok){
            ans[x][j]=ans[x+1][j]=Red;
            return;
        }
    }
    for(register int i=x-1;i<=x+2;++i)
        if(!a[i][3])
            ans[i][3]=Red;
    if(a[x-1][3]){
        ans[x-1][2]=Blue,
        ans[x][4]=Red;
    }
    if(a[x+2][3]){
        ans[x+2][2]=Blue,
        ans[x+1][4]=Red;
    }
    if(a[x][3] || a[x+1][3]){
        ans[x][2]=ans[x+1][2]=Red;
    }
}

inline void buildroad(){
    int fr=0,ls=0;
    for(register int i=1;i<=n;++i)
        if(ans[i][m]==Red){
            if(!fr) fr=i;
            ls=i;
        }
    if(!fr || (ls>3 && fr<n-2)) return;
    if(ls<=3 && a[4][m-1]==Blue){
        ans[3][m]=ans[4][m]=ans[5][m]=Red;
        return;
    }
    if(fr>=n-2 && a[n-3][m-1]==Blue){
        ans[n-4][m]=ans[n-3][m]=ans[n-2][m]=Red;
        return;
    }
    int x=(ls<=3?2:n-2);
    for(register int i=x;i<=x+1;++i)
        for(register int j=m-1;j<=m;++j)
            if(!a[i][j])
                ans[i][j]=Red;
}

bool End;
#define File ""
signed main(){
    // #ifndef ONLINE_JUDGE
    // freopen(File ".in","r",stdin);
    // freopen(File ".out","w",stdout);
    // #endif
    for(register int T=read();T;--T,clear()){
        n=read(),m=read();
        for(register int i=1;i<=n;++i)
            for(register int j=1;j<=m;++j)
                a[i][j]=ans[i][j]=reads();
        int tmp=calc();
        if(tmp>=4){
            puts("NO");
            continue;
        }
        if(tmp>0) while(!Nice()) rotate();
        Blue=ans[1][1],Red=Blue^1;
        for(register int i=2;i<n;++i)
            for(register int j=2;j<m;++j)
                if(!a[i][j])
                    ans[i][j]=(i%4>1?Blue:Red);
        for(register int i=1;i<n;++i)
            if(ans[i][m-1]==ans[i+1][m] && ans[i+1][m-1]==ans[i][m] && ans[i][m]!=ans[i+1][m]){
                if(!a[i][m]) ans[i][m]^=1;
                else ans[i+1][m]^=1;
            }
        buildroad();
        for(register int i=2;i<m;++i){
            if(a[2][i]==Red) findroad(2,i);
            if(a[n-1][i]==Red) findroad(n-1,i);
        }
        for(register int i=6;i<=n-6;i+=4)
            if(ans[i][m]==Blue || ans[i+1][m]==Blue)
                bigroad(i);
        while(cntr%4!=0) rotate();
        puts("YES");
        for(register int i=1;i<=n;++i){
            for(register int j=1;j<=m;++j)
                write(ans[i][j]);
            putchar('\n');
        }
    }
    return 0;
}
  • 标题: CF1667F Yin Yang
  • 作者: Arahc
  • 创建于 : 2022-06-25 08:00:00
  • 更新于 : 2023-03-15 02:54:32
  • 链接: https://arahc.github.io/2022/06/25/【题解】CF1667F-Yin-Yang/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
CF1667F Yin Yang
  1. 题面
  2. 题解
  3. 代码