推荐自己跟着写自己的代码食用,而不是复制粘贴。=)
这篇文章基本来自《Ray Tracing in One Weekend》。
你的第一幅作品
ppm 图片格式
ppm 是一个简单的图像格式:
ppm 格式是一种图片格式,全名 Portable PixelMap。PPM格式的图片如果用文本编辑器打开会发现都是 ASCII 码而不是二进制。所以这种格式的图片方便操作,但是文件大小可能不是很友好。
ppm 的格式如下:
1 2 3 4 5 6 P3 m n 255 r g b r g b ...
其中 m , n m,n m , n r , g , b r,g,b r , g , b
Hello World!
那么就尝试写一个代码试试吧:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <iostream> int main () int n = 256 , m = 256 ; std::cout << "P3\n" << m << " " << n << "\n255\n" ; for (int i = 0 ; i < n; ++i) for (int j = 0 ; j < m; ++j) { int r = 0 ; int g = i; int b = j; std::cout << r << " " << g << " " << b << "\n" ; } return 0 ; }
跑一下,把输出保存成 xxx.ppm,然后打开,应该会长这样:
如果你无法打开 ppm 格式的图片文件,可以在 VSCode 装 simple ppm viewer 插件,或者在线查看器,或者使用如下 python 程序(python <python-file-name> <input-image> <output-image>)把 ppm 格式的图片文件导出成 jpg 或 png(deepseek 写的):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 from PIL import Imageimport argparsedef convert_ppm (input_path, output_path ): try : img = Image.open (input_path) img.save(output_path) except Exception as e: raise RuntimeError(f"Failed to transform: {e} " ) if __name__ == "__main__" : parser = argparse.ArgumentParser() parser.add_argument("input" ) parser.add_argument("output" ) args = parser.parse_args() convert_ppm(args.input , args.output)
简单图像渲染
为了方便,请你掏出你尘封已久的 三维计算几何的三维向量 类。这里假设你已经实现好了三维向量类并且有一些基本数学计算的功能。
另外,我们还需要一个 color 类,为了方便偷懒,我们钦定颜色类的三个参数取值为 [ 0 , 1 ] [0,1] [ 0 , 1 ] using Color = Vector3<double> 了。最好,再实现一个把 color 类输出的函数。
假设将三维向量类和颜色类分别封装在 Vector3.hpp 和 Color.hpp 中,那么可以改写第一部分中我们的第一个程序为一个更工程的实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 #include "Vector3.hpp" #include "Color.hpp" int main () int n = 256 , m = 256 ; std::cout << "P3\n" << n << " " << m << "\n255\n" ; for (int i = 0 ; i < n; ++i) for (int j = 0 ; j < m; ++j) { Color c = Color (0 , double (i)/(n-1 ), double (j)/(m-1 )); printColor (std::cout, c); } return 0 ; }
这个程序的运行结果应当要和上面例子里的图片一样。
虚拟视口
通常情况下,我们并不只需要 256 × 256 256\times 256 2 5 6 × 2 5 6 1 : 1 1:1 1 : 1 16 : 9 16:9 1 6 : 9
实现方法很简单,我们可以设置一个宽高比和图片的宽度(或高度),然后计算图片的高度(或宽度)。需要避免非常极端的数据,导致图片另一维没有数据(如高度为零)。
但由于我们要用(最好用)int 去存图片的大小,所以这时候我们设置的宽高比 16 : 9 16:9 1 6 : 9
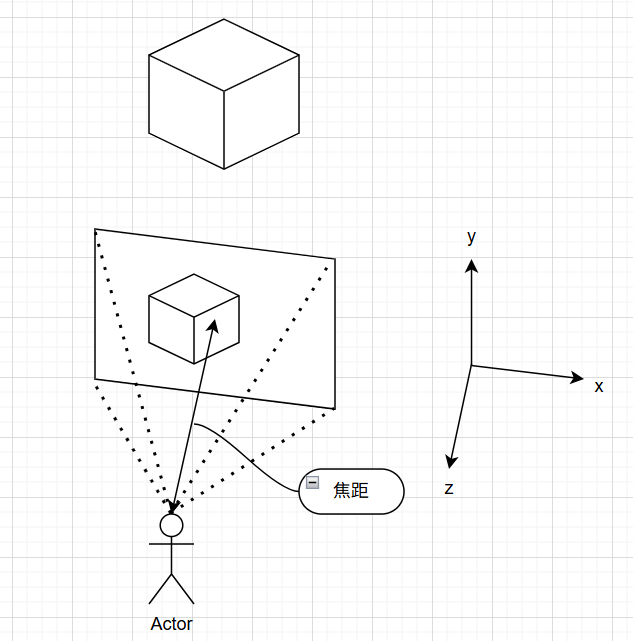
我们希望构建一个假想的“屏幕”,作为一个虚拟视口,在这个屏幕上显示我们能看到的东西:
那么我们需要设置这个屏幕的期望宽高比,以及这个屏幕的大小。在后续的代码里,我设定的宽高比为 16 : 9 16:9 1 6 : 9 800 × 450 800\times 450 8 0 0 × 4 5 0
为了方便应对不同大小的情况,最好不要在程序的各个地方散落屏幕的实际大小 800 × 450 800\times 450 8 0 0 × 4 5 0 将屏幕的高度统一为 2 2 2 [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] (即向量单位化之后,任意一维的取值范围),宽度依然用高度和宽高比计算。
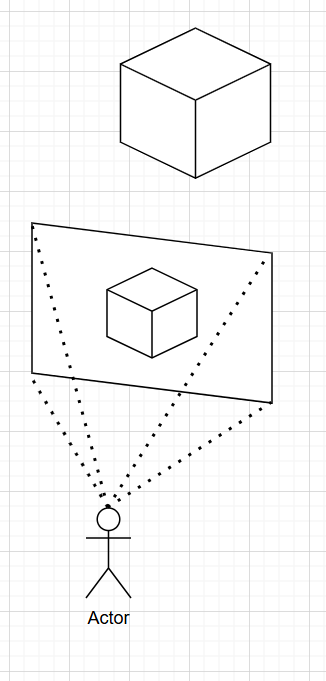
接下来我们需要一个摄像机,也就是图片中的演员。显然,为了方便,将摄像机设置为空间的原点。为了符合数学和物理直觉,我们建右手系(Unity 里面建的是左手系,那很抽象了)。为了一些原因,我们设置 y y y x x x z z z 负 方向指向虚拟视口。此外,定义摄像机到虚拟视口的长度为焦距,这个值我们设为 1 1 1
架好摄像机
为了能让我们看到东西,上帝说,要有光。
一束光线,在正常理解中应该是一条射线。用 R ( t ) : A + t v ⃗ R(t): A+t\vec v R ( t ) : A + t v t ⩾ 0 t\geqslant 0 t ⩾ 0 A A A v ⃗ \vec v v t t t
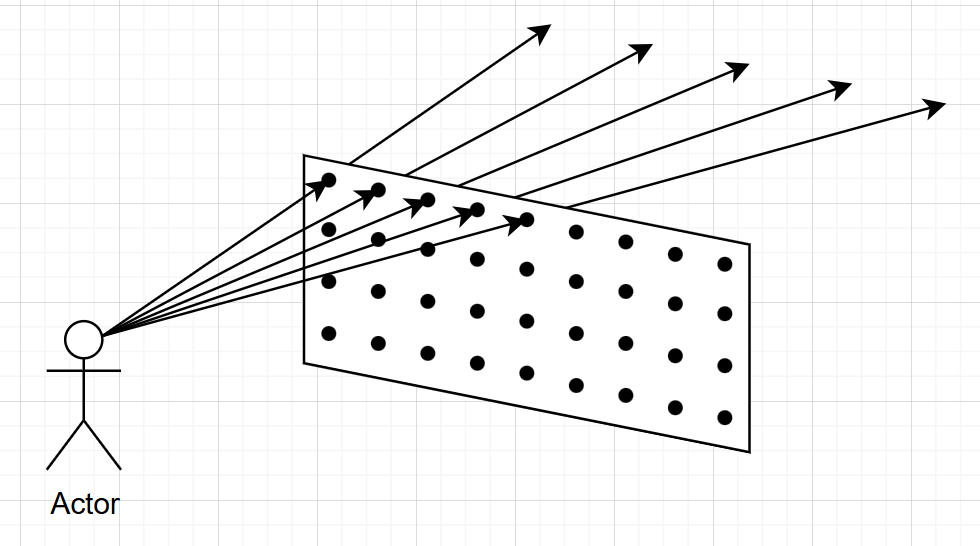
下面我们考虑从一个固定点(摄像机)出发,发出的光线(视线),因为我们已经有了虚拟视口的宽度和高度了,那么对于每个像素点,我们都可以引出一条光线(下图只画了五条,仅作示例):
对于每条光线,我们其实在考虑下面的问题:找到这条光线和空间中物体的交点,并提取第一个交点处的颜色信息。把这个颜色信息作为对应像素点的颜色呈现出来。
那么到目前为止,可以写出下面的程序。我们期望使用函数 getRayColor 来实现找到一条光线和空间中和物体第一次相交的交点的颜色。不过我们可以先画画简单的东西试试,比如一个渐变(程序中的 _White, _Blue 是我定义的常颜色):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include "Color.hpp" #include "Ray.hpp" #include "Vector3.hpp" Color getRayColor (const Ray &ray) { double k = ray.dir.x * ray.dir.x + ray.dir.y * ray.dir.y; return (1 - k) * _White + k * _Blue; } int main () double expectRatio = 16.0 / 9.0 ; int width = 800 ; int height = std::max (1 , (int )(width / expectRatio)); double viewHeight = 2.0 ; double viewWidth = (double )(width) / height * viewHeight; double focalLengh = 1.0 ; Vec3 cameraPos (0 , 0 , 0 ) ; Vec3 deltaX = Vec3 (viewWidth / width, 0 , 0 ); Vec3 deltaY = Vec3 (0 , -viewHeight / height, 0 ); Vec3 pixUpLeftPos = cameraPos - Vec3 (viewWidth / 2 , -viewHeight / 2 , focalLengh) + 0.5 * (deltaX + deltaY); std::cout << "P3\n" << width << " " << height << "\n255\n" ; for (int i = 0 ; i < height; ++i) for (int j = 0 ; j < width; ++j) { Vec3 pixPos = pixUpLeftPos + deltaX * j + deltaY * i; Vec3 rayDir = (pixPos - cameraPos).unit (); Ray ray (cameraPos, rayDir) ; Color col = getRayColor (ray); printColor (std::cout, col); } return 0 ; }
大概的逻辑就是先设置好视口,然后架一台摄像机,为了方便,计算相邻两个像素点之间的位移和整个视口的左上角的像素的位移,这样就可以根据当前的视口坐标 ( i , j ) (i,j) ( i , j ) picPos,从而确定光线。
对于得到的图案,可以先理论分析一下,由于我们单位化了光线的方向向量,所以 x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x 2 + y 2 + z 2 = 1 x 2 + y 2 x^2+y^2 x 2 + y 2 z = 1 z=1 z = 1 z = 0 z=0 z = 0
实际效果也是如此:
简单的实例:球
下面我们开始真的考虑在坐标系里面加点东西。出于简单,先试试加一个球体。
我们都知道球心在 C ( x c , y c , z c ) C(x_c,y_c,z_c) C ( x c , y c , z c ) r r r ( x − x c ) 2 + ( y − y c ) 2 + ( z − z c ) 2 = r 2 (x-x_c)^2+(y-y_c)^2+(z-z_c)^2=r^2 ( x − x c ) 2 + ( y − y c ) 2 + ( z − z c ) 2 = r 2 R : A + t v ⃗ R: A+t\vec v R : A + t v A A A P = A + t v ⃗ P=A+t\vec v P = A + t v
( C − ( A + t v ⃗ ) ) ⋅ ( C − ( A + t v ⃗ ) ) = r 2 ⇒ t 2 v ⃗ ⋅ v ⃗ − 2 t v ⃗ ⋅ ( C − A ) + ( C − A ) ⋅ ( C − A ) − r 2 = 0 ⇒ { t = − b ± b 2 − 4 a c 2 a a = v ⃗ ⋅ v ⃗ b = − 2 v ⃗ ⋅ ( C − A ) c = ( C − A ) ⋅ ( C − A ) − r 2 \begin{aligned}
& (C-(A+t\vec v))\cdot(C-(A+t\vec v)) = r^2 \\
\Rightarrow& t^2\vec v\cdot\vec v - 2t\vec v\cdot(C-A) + (C-A)\cdot(C-A) - r^2 = 0 \\
\Rightarrow& \begin{cases}
t = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \\
a = \vec v\cdot\vec v \\
b = -2\vec v\cdot(C-A) \\
c = (C-A)\cdot(C-A)-r^2
\end{cases}
\end{aligned}
⇒ ⇒ ( C − ( A + t v ) ) ⋅ ( C − ( A + t v ) ) = r 2 t 2 v ⋅ v − 2 t v ⋅ ( C − A ) + ( C − A ) ⋅ ( C − A ) − r 2 = 0 ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ t = 2 a − b ± b 2 − 4 a c a = v ⋅ v b = − 2 v ⋅ ( C − A ) c = ( C − A ) ⋅ ( C − A ) − r 2
实际上,这个结果可以稍微化简一下,卡个常数:
{ a = v ⃗ ⋅ v ⃗ h : = v ⃗ ⋅ ( C − A ) b = − 2 h c = ( C − A ) ⋅ ( C − A ) − r 2 ⇒ t = − b ± b 2 − 4 a c 2 a = 2 h ± 4 h 2 − 4 a c 2 a = h ± h 2 − a c a \begin{aligned}
& \begin{cases}
a = \vec v\cdot\vec v \\
h:= \vec v\cdot(C-A) \\
b = -2h \\
c = (C-A)\cdot(C-A)-r^2
\end{cases} \\
\Rightarrow t &= \frac{-b\pm\sqrt{b^2-4ac}}{2a} \\
&= \frac{2h\pm\sqrt{4h^2-4ac}}{2a} \\
&= \frac{h\pm\sqrt{h^2-ac}}{a}
\end{aligned}
⇒ t ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ a = v ⋅ v h : = v ⋅ ( C − A ) b = − 2 h c = ( C − A ) ⋅ ( C − A ) − r 2 = 2 a − b ± b 2 − 4 a c = 2 a 2 h ± 4 h 2 − 4 a c = a h ± h 2 − a c
于是我们可以针对一个球,计算光线是否和球相交,若相交,还能得出一个合法的 t t t
由于后续可能会加入更多的球,或其他什么乱七八糟的形状,我们充分发挥 C++ 的多态,设置一个父类(基类)来统称这些玩意。最开始我是想把类型命名为 Object 的,但是考虑到实际游戏里有很多东西不能被光线探测到,比如空气和碰撞箱,所以不会命名了。然而《Ray Tracing in One Weekend》这本书里面给出了一个很妙的方式:为了体现这些物体是会被光线击中的这一特性,命名为 Hittable.
在父类 Hittable 下定义子类球体,即 Sphere:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Hittable { public : virtual double hit (const Ray &ray) const 0 ; }; class Sphere : public Hittable { public : Vec3 C; double r; Sphere (const Vec3 &_C = Vec3 (0 , 0 , 0 ), double _r = 0 ) : C (_C), r (_r) {} double hit (const Ray &ray) const override double a = dot (ray.dir, ray.dir); double h = dot (ray.dir, C - ray.A); double c = dot (C - ray.A, C - ray.A) - r * r; double delta = h * h - a * c; if (delta < 0 ) return -1 ; double sqDelta = std::sqrt (delta); if (h + sqDelta < 0 ) return -1 ; return (h <= sqDelta ? (h + sqDelta) / a : (h - sqDelta) / a); } };
现在的球没有任何颜色,非常的单调,我们可以想一个好的方法给球上一个花里胡哨的颜色。例如,我们取光线和球的交点处在球表面上的向外的法向量并单位化,那么单位化后的法向量,x , y , z x,y,z x , y , z [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] r , g , b r,g,b r , g , b
关于法向量的计算,显然,法向量的方向就是 P − C P-C P − C
这里引入法向量,因为想想也觉得是,我们后面肯定会需要用到交点在面上的法向量去算一些东西的。
底色(即没有击中物体的光线的颜色)直接采用你喜欢的渐变色即可(请注意,这个程序实现的渐变不是 垂直渐变):
1 2 3 4 5 6 7 8 9 10 11 Sphere S (Vec3(0 , 0 , -2 ), 0.5 ) ;Color getRayColor (const Ray &ray) { double t = S.hit (ray); if (t >= 0 ){ Vec3 n = (ray.at (t) - S.C).unit (); return 0.5 * Color (n.x + 1 , n.y + 1 , n.z + 1 ); } double k = 0.5 * (ray.dir.y + 1 ); return (1 - k) * _White + k * Color (0.7 , 0.7 , 1 ); }
那么得到的图案应该是:
实例集合封装
为了方便我们实现一大堆的实例的碰撞检测,我们可以考虑封装一个实例集合。为了方便不区分地直接使用 hit 去判定一个光线是否和这个这个集合内地某个实例相交,我们干一个可能反人类地操作:把这个集合视为 Hittable 的一个子类。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 using std::make_shared;using std::shared_ptr;class HittaleSet : public Hittable { public : std::vector<shared_ptr<Hittable>> vec; HittaleSet () {} void clear () vec.clear (); } void insert (shared_ptr<Hittable> obj) vec.push_back (obj); } double hit (const Ray &ray) const override double t = -1 ; for (const auto &x : vec) { double res = x->hit (ray); if (res >= 0 && (t < 0 || res < t)) t = res; } return t; } };
由于 Hittable 是一个父类(基类),如果你往里面加入子类对象的时候,会触发切片,导致只有父类自己的内容会被保留,子类自定义的东西就没有了。你的子类的 hit 函数就会原地蒸发。
因此,我们用 shared_ptr,不能直接使用 vector<Hittable>.
摄像头封装
同样的,考虑到很可能不仅仅使用一个固定在原点的摄像头,我们需要封装一个摄像头类。这一段很轻松,其实就是把主函数的东西移植到类里面。
……想法很美好,但我们很快发现主函数里面的有一个东西是难以改造的:
1 2 3 4 5 6 7 8 9 10 11 Sphere S (Vec3(0 , 0 , -2 ), 0.5 ) ;Color getRayColor (const Ray &ray) { double t = S.hit (ray); if (t >= 0 ){ Vec3 n = (ray.at (t) - S.C).unit (); return 0.5 * Color (n.x + 1 , n.y + 1 , n.z + 1 ); } double k = 0.5 * (ray.dir.y + 1 ); return (1 - k) * _White + k * Color (0.7 , 0.7 , 1 ); }
这个部分,尤其是计算法向量的部分,是针对了对应的物体是一个球计算的。但实际上,我们需要支持更多类型的实例时,就不能单纯这么算了。球有球的法向量算法,正方体有正方体的,各有各的,而且传入的类型的 Hittable,所以怎么算法向量还得额外判断对应的子类。
这实在是太麻烦了,所以我们需要附带改进一下 hit 函数,使得其同时返回切点和对应的法向量。一种经典而且常数更小的方法是,自定义一个返回值类型,比如 hitResult,给 hit 函数传入一个 hitResult 类型的变量的地址,去把结果存到这个变量里。当然也可以直接返回 hitResult 类型,但是常数更大。因此这里采用前者。
hitResult 类型里,目前只需要两个变量,一个 t t t n ⃗ \vec n n t = − 1 t=-1 t = − 1 hit 函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 bool hit (const Ray &ray, hitResult &res) const override hitResult tmp; bool ret = false ; for (const auto &x : vec) if (x->hit (ray, tmp) && (res.t < 0 || tmp.t < res.t)){ res = tmp; ret = true ; } return ret; } bool hit (const Ray &ray, hitResult &res) const override double a = dot (ray.dir, ray.dir); double h = dot (ray.dir, C - ray.A); double c = dot (C - ray.A, C - ray.A) - r * r; double delta = h * h - a * c; if (delta < 0 ) return false ; double sqDelta = std::sqrt (delta); if (h + sqDelta < 0 ) return false ; res.t = h <= sqDelta ? (h + sqDelta) / a : (h - sqDelta) / a; res.n = (ray.at (res.t) - C).unit (); return true ; }
这样我们就可以实现摄像机类了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Camera { private : double expectRatio; int width, height; double viewHeight, viewWidth; double focalLength; Vec3 pos; Vec3 deltaX, deltaY, pixUpLeftPos; Color getRayColor (const Ray &ray, const Hittable &objs) { hitResult res; if (objs.hit (ray, res)) return 0.5 * Color (res.n.x + 1 , res.n.y + 1 , res.n.z + 1 ); double k = 0.5 * (ray.dir.y + 1 ); return (1 - k) * _White + k * Color (0.7 , 0.7 , 1 ); } public : Camera (double _expectRatio = 16.0 / 9.0 , int _width = 800 , double _viewHeight = 2.0 , double _focalLength = 1.0 , Vec3 _pos = Vec3 (0 , 0 , 0 )) : expectRatio (_expectRatio), width (_width), height (std::max (1 , (int )(_width / _expectRatio))), viewHeight (_viewHeight), viewWidth ((double )(_width) / height * viewHeight), focalLength (_focalLength), pos (_pos), deltaX (viewWidth / width, 0 , 0 ), deltaY (0 , -viewHeight / height, 0 ), pixUpLeftPos (_pos - Vec3 (viewWidth / 2 , -viewHeight / 2 , focalLength) + 0.5 * (deltaX + deltaY)) {} void render (const Hittable &objs) std::cout << "P3\n" << width << " " << height << "\n255\n" ; for (int i = 0 ; i < height; ++i) for (int j = 0 ; j < width; ++j) { Vec3 pixPos = pixUpLeftPos + deltaX * j + deltaY * i; Vec3 rayDir = (pixPos - pos).unit (); Ray ray (pos, rayDir) ; Color col = getRayColor (ray, objs); printColor (std::cout, col); } } };
随后我们的主函数大大简化:
1 2 3 4 5 6 7 int main () HittaleSet objs; objs.insert (make_shared <Sphere>(Vec3 (0 , 0 , -2 ), 0.5 )); Camera cam (16.0 / 9.0 , 800 , 2.0 , 1.0 , Vec3(0 , 0 , 0 )) ; cam.render (objs); return 0 ; }
运行主函数,应该会得到和前面一样的彩色球的图案。
抗锯齿
即使你不放大那个彩球图象也会发现,那张图的锯齿化非常严重。这是因为每个像素要么对应的光线打到球上了,此时整个像素的颜色就是那一条打到球上的光线的颜色,要么没有打到,取背景色。用一条光线独断导致边界像素突出。
那么就有了一个抗锯齿的大致的方向:就是让像素的颜色稍微“中和”一下,使得边界处的颜色过渡稍微平缓。
注意到对于每个像素方格,我们只取了格子的正中心的一个点,读取这个点对应的光线的颜色。结合上面的思想,我们可以换成采样:在这个格子(或比这个格子稍大一点的范围,设置合理即可)内额外采样一些点去得到一个,把这些颜色平均起来。这样子一个像素点对应的颜色期望下应该是这个像素对应的实际范围的一个“平均”颜色。
为此,我们需要给摄像机加入一个新的参数 nSample 表示单个像素的额外采样量。
为了实现随机,我新建了一个头文件 Math.hpp,将和数学有关的操作和常量(包括之前的计算几何全家桶)放进去。在里面我实现了随机数生成器和辅助函数,由于实现简单,此处忽略。
下面是修改后的渲染,我设置的范围比这个像素格子的大小稍大一点:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Color getSampleColor (const Vec3 &pixPos, const Hittable &objs) { Vec3 samPos = pixPos + deltaX * rnd.rand <double >(-0.7 , 0.7 ) + deltaY * rnd.rand <double >(-0.7 , 0.7 ); Ray ray (pos, (samPos - pos).unit()) ; return getRayColor (ray, objs); } void render (const Hittable &objs) double sampleRatio = 1.0 / (nSample + 1 ); std::cout << "P3\n" << width << " " << height << "\n255\n" ; for (int i = 0 ; i < height; ++i) for (int j = 0 ; j < width; ++j) { Vec3 pixPos = pixUpLeftPos + deltaX * j + deltaY * i; Ray ray (pos, (pixPos - pos).unit()) ; Color col = getRayColor (ray, objs); for (int k = 0 ; k < nSample; ++k) col += getSampleColor (pixPos, objs); col *= sampleRatio; printColor (std::cout, col); } }
将采样数设置为 50 50 5 0
自行放大和上一张彩色球图片对比,可以发现抗锯齿发挥作用了。
光追
材料类
我们希望能实现不同材质的球,有些只是单纯的球(触发漫反射),有些可能是镜面球,有些可能是玻璃球……球的种类影响光线的逻辑。所以我们需要一个材料类来管理不同的材料。
一个材料的信息应该包含:如果给定入射光线、法向量等信息(hitResult),会不会产生反射光线,如果会,会产生怎样的反射光线,又吸收了多少光线。
1 2 3 4 class Material { public : virtual bool scatter (const Ray &rayIn, const hitResult &res, Color &attn, Ray &rayOut) const 0 ; };
hitResult 中需要添加光线碰到的实例的材料信息,但是材料类里面也用到了 hitResult,为了避免头文件互相引用或者其他冲突,在 hitResult 对应的头文件中,只声明材料类,不引用材料类头文件即可。
然后我们修改 getRayColor 的逻辑,为了避免大量的反射导致超绝递归,我们还要给摄像头类设置一个最大递归深度,如果超过这个递归深度,则视为没有光(黑色),调用 getRayColor 时,dep 的值设置为最大递归深度:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 Color getRayColor (const Ray &ray, const Hittable &objs, int dep) { if (dep == 0 ) return _Black; hitResult res; if (objs.hit (ray, res)) { Ray scat; Color attn; if (res.mat->scatter (ray, res, attn, scat)) return atten * getRayColor (scat, objs, dep - 1 ); return _Black; } double k = 0.5 * (ray.dir.y + 1 ); return (1 - k) * _White + k * Color (0.7 , 0.7 , 1 ); }
别忘记在球的类型中,添加球的材质。
漫反射(郎伯模型)
现在我们实现一个会进行漫反射的材料。当光线照射到漫反射材料的时候,我们用郎伯模型去计算反射情况:
假设物体表面平滑,入射光完全漫反射后在所有方向的辐射亮度相同,漫反射的光强和入射角的余弦成正比,和反射方向无关。
需要注意的是,虽然我们代码实现是从摄像头发出光线的,但事实显然并非如此,是光线反射到摄像头的。请不要弄反入射角和反射角。
我们可以用如下方法轻松地构造和入射角(从摄像头的视角,或许是“反射角”?)的余弦成正比分布的随机光线:
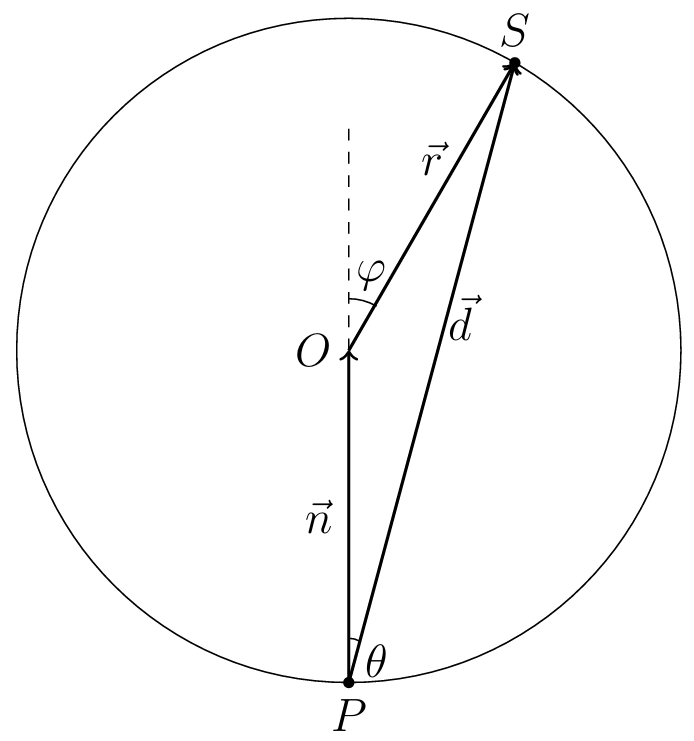
得到交点 P P P n ⃗ \vec n n O = P + n ⃗ O=P+\vec n O = P + n O O O
取单位球上随机一个不为 P P P S S S
连接 P S PS P S P S PS P S
以上是示意图。
以 n ⃗ \vec n n <path d='M377 20c0-5.333 1.833-10 5.5-14S391 0 397 0c4.667 0 8.667 1.667 12 53.333 2.667 6.667 9 10 19 6.667 24.667 20.333 43.667 41 57 7.333 4.667 1110.667 11 18 0 6-1 10-3 12s-6.667 5-14 9c-28.667 14.667-53.667 35.667-75 63-1.333 1.333-3.167 3.5-5.5 6.5s-4 4.833-5 5.5c-1 .667-2.5 1.333-4.5 2s-4.333 1-7 1c-4.667 0-9.167-1.833-13.5-5.5S337 184 337 178c0-12.667 15.667-32.333 47-59H213l-171-1c-8.667-6-13-12.333-13-19 0-4.667 4.333-11.333 13-20p class='h3'59c-16-25.333-24-45-24-59z'/> S S S φ \varphi φ ϕ \phi ϕ φ \varphi φ
d A = 2 π sin φ d φ \mathrm{d} A = 2\pi\sin\varphi\,\mathrm{d}\varphi d A = 2 π sin φ d φ
球的表面积为 4 π 4\pi 4 π φ 0 \varphi_0 φ 0 [ φ , φ + d φ ] [\varphi,\varphi+\mathrm{d}\varphi] [ φ , φ + d φ ]
d A 4 π = sin φ 2 d φ = sin ( 2 θ ) d θ \frac{\mathrm{d}A}{4\pi} = \frac{\sin\varphi}{2}\,\mathrm{d}\varphi = \sin(2\theta)\,\mathrm{d}\theta 4 π d A = 2 sin φ d φ = sin ( 2 θ ) d θ
对于给定 θ \theta θ ϕ \phi ϕ
d Ω = 2 π sin θ d θ \mathrm{d}\Omega = 2\pi\sin\theta\,\mathrm{d}\theta d Ω = 2 π sin θ d θ
于是得到概率密度
p = sin ( 2 θ ) d θ d Ω = cos θ π ∝ cos θ p = \frac{\sin(2\theta)\,\mathrm{d}\theta}{\mathrm{d}\Omega} = \frac{\cos\theta}{\pi}\propto \cos\theta p = d Ω sin ( 2 θ ) d θ = π cos θ ∝ cos θ
显然,漫反射本身还要吸收一些光,在这里我们先随便设置一个默认吸收量,例如 50 % 50\% 5 0 % S S S P P P
根据以上理论,建立发生漫反射的材料 Diffuse 类:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Diffuse : public Material { private : Color attenCol; public : Diffuse () : attenCol (1 , 1 , 1 ) {} Diffuse (const Color &_attenCol) : attenCol (_attenCol) {} bool scatter (const Ray &rayIn, const hitResult &res, Color &atten, Ray &rayOut) const override Vec3 realN = dot (rayIn.dir, res.n) > 0 ? -res.n : res.n; Vec3 outDir = (realN + rnd.randUnit ()).unit (); if (outDir.nearZero ()) outDir = realN; rayOut = Ray (rayIn.at (res.t), outDir); atten = attenCol; return true ; } };
由于我们目前还只有一个球,为了方便检查,我们增加一个巨大的球,用来假装是地面。我设置小球为 C : ( 0 , 0 , − 2 ) , r = 0.5 C:(0,0,-2),r=0.5 C : ( 0 , 0 , − 2 ) , r = 0 . 5 C : ( 0 , − 100.5 , − 2 ) , r = 100 C:(0,-100.5,-2),r=100 C : ( 0 , − 1 0 0 . 5 , − 2 ) , r = 1 0 0 70 % 70\% 7 0 % 30 % 30\% 3 0 %
可以勉强看到接触部分有更深的阴影。
阴影失真
为什么这个东西明明只有 30 % 30\% 3 0 %
《Ray Tracing in One Weekend》提到了这样的阴影失真 的问题。这是一个非常小但后果很严重的错误:我们使用 at 试图得到光线和球体表面的交点 P P P P P P
由于浮点数误差难以避免,所以一个比较好的解决这个问题的方案是:直接忽略和出发点非常接近的交点。
我们定义区间类 Interval,包含 l , r l,r l , r [ l , r ] [l,r] [ l , r ] hit 函数和 getRayColor 函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 bool hit (const Ray &ray, Interval rangeT, hitResult &res) const override hitResult tmp; double nowR = rangeT.r; for (const auto &x : vec) if (x->hit (ray, Interval (rangeT.l, nowR), tmp) && (res.t < 0 || tmp.t < res.t)) { nowR = tmp.t; res = tmp; } return rangeT.contain (res.t); } bool hit (const Ray &ray, Interval rangeT, hitResult &res) const override double a = dot (ray.dir, ray.dir); double h = dot (ray.dir, C - ray.A); double c = dot (C - ray.A, C - ray.A) - r * r; double delta = h * h - a * c; if (delta < 0 ) return false ; double sqDelta = std::sqrt (delta); double t1 = (h - sqDelta) / a, t2 = (h + sqDelta) / a; if (rangeT.contain (t1)) res.t = t1; else if (rangeT.contain (t2)) res.t = t2; else return false ; res.n = (ray.at (res.t) - C).unit (); res.mat = mat; return true ; }
getRayColor 函数只是在 hit 判断中多传入一个区间参数 [ ε 0 , + ∞ ] [\varepsilon_0,+\infty] [ ε 0 , + ∞ ] ε 0 = 1 0 − 4 \varepsilon_0=10^{-4} ε 0 = 1 0 − 4
可以发现,球过黑问题有明显改善。
关于为什么我们的球没有设置颜色,但是它渲染出来看起来是淡紫色的,因为我的例子中,背景板是紫色的。
Gamma 校正
虽然这个球已经很亮了,但那是对比的阴影失真的版本。实际上,反射率 70 % 70\% 7 0 %
存在一些客观因素导致人眼看到的亮度和计算机实际意图显示的亮度并不是线性对等关系。即你给它输入 x ( 0 ⩽ x ⩽ 1 ) x\,(0\leqslant x\leqslant 1) x ( 0 ⩽ x ⩽ 1 ) y ( 0 ⩽ y ⩽ 1 ) y\,(0\leqslant y\leqslant 1) y ( 0 ⩽ y ⩽ 1 ) y = x y=x y = x y y y y 1 = x γ y_1=x^\gamma y 1 = x γ γ \gamma γ 2.2 2.2 2 . 2 x x x y 2 = x 1 γ y_2=x^{\frac{1}{\gamma}} y 2 = x γ 1
我们目前输出图像是线性空间内的,所以渲染出来的东西其实在数据上是对的,但是肉眼看起来上和数据相比偏暗。因此我们需要进行 Gamma 补正。这非常好实现,在此忽略修改代码。
我们会得到反射率为 70 % 70\% 7 0 %
镜面反射
镜面反射的逻辑比漫反射好实现得多。那为什么先说漫反射呢,废话,一个全是镜子的图我还看个啥,看不动啊。
由显然的公式,当然画个图也可以知道,已知入射光线方向向量 v ⃗ \vec v v n ⃗ \vec n n v ⃗ − 2 ( v ⃗ ⋅ n ⃗ ) n ⃗ \vec v - 2(\vec v\cdot\vec n)\vec n v − 2 ( v ⋅ n ) n
为了方便起见,我们定义的镜子材料还是可能存在颜色吸收的。默认为全反射。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Mirror : public Material { private : Color attenCol; public : Mirror () : attenCol (1 , 1 , 1 ) {} Mirror (const Color &_attenCol) : attenCol (_attenCol) {} bool scatter (const Ray &rayIn, const hitResult &res, Color &atten, Ray &rayOut) const override Vec3 realN = dot (rayIn.dir, res.n) > 0 ? -res.n : res.n; Vec3 outDir = rayIn.dir - 2 * dot (rayIn.dir, realN) * realN; rayOut = Ray (rayIn.at (res.t), outDir); atten = attenCol; return true ; } };
我们使用复杂一点的球来测试程序,例如:
1 2 3 4 5 6 7 8 9 10 int main () HittaleSet objs; objs.insert (make_shared <Sphere>(make_shared <Diffuse>(Color (0.5 , 0.6 , 0.7 )), Vec3 (0 , 0.1 , -2 ), 0.5 )); objs.insert (make_shared <Sphere>(make_shared <Diffuse>(Color (0.3 , 0.3 , 0.3 )), Vec3 (0 , -100.5 , -2 ), 100 )); objs.insert (make_shared <Sphere>(make_shared <Mirror>(), Vec3 (-1 , 0.5 , -2 ), 0.4 )); objs.insert (make_shared <Sphere>(make_shared <Mirror>(Color (0.9 , 0.5 , 0.3 )), Vec3 (1 , 0 , -1.5 ), 0.3 )); Camera cam (16.0 / 9.0 , 800 , 2.0 , 1.0 , Vec3(0 , 0 , 0 ), 50 , 10 ) ; cam.render (objs); return 0 ; }
第一个球是一个有颜色的漫反射球,第二个球为地面,第三个球为全反射镜子球,第四个球为有光线吸收的带颜色的镜子球。渲染的结果如下:
铜镜:模糊反射
金属的表面通常并非和现代的镜子一样可以进行完全的镜面反射,而是模糊的。
为了实现模糊效果,我们可以不把反射光线的方向唯一确定地算出来,而是在原来的基础上加上一个随机扰动,这样反射光线就会在一个区域内,从而实现平均效果,也就实现了模糊效果。
由于模糊反射的代码实现和镜面反射高度相似,我们可以考虑把它们结合起来。我们把 Mirror 类重命名为反光物体类 Glossy,加入一个新的参数 f u z z fuzz f u z z f u z z = 0 fuzz=0 f u z z = 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Glossy : public Material { private : Color attenCol; double fuzz; public : Glossy (double _fuzz = 0 ) : attenCol (1 , 1 , 1 ), fuzz (_fuzz) {} Glossy (const Color &_attenCol, double _fuzz = 0 ) : attenCol (_attenCol), fuzz (_fuzz) {} bool scatter (const Ray &rayIn, const hitResult &res, Color &atten, Ray &rayOut) const override Vec3 realN = dot (rayIn.dir, res.n) > 0 ? -res.n : res.n; Vec3 outDir = rayIn.dir - 2 * dot (rayIn.dir, realN) * realN + fuzz * rnd.randUnit (); if (dot (outDir, realN) < 0 ) return false ; rayOut = Ray (rayIn.at (res.t), outDir.unit ()); atten = attenCol; return true ; } };
我们试试把上述例子的有色镜子球改成有色的 f u z z = 0.3 fuzz=0.3 f u z z = 0 . 3
玻璃:折射
清澈透明的材料会发生光的折射,例如玻璃。当然其实是可能会同时发生折射和反射,也可能只有反射(全反射)。以上都是初中物理内容,只在必要时作提及。
这样的材料有一个折射率。光从折射率 η \eta η η ′ \eta' η ′ θ \theta θ θ ′ \theta' θ ′
η η ′ = sin θ ′ sin θ \frac{\eta}{\eta'} = \frac{\sin\theta'}{\sin\theta}
η ′ η = sin θ sin θ ′
我们希望用向量的方式算出来,现在有入射光线的方向向量 v ⃗ \vec v v n ⃗ \vec n n d ⃗ \vec d d
η ( v ⃗ × n ⃗ ) = η ′ ( d ⃗ × n ⃗ ) ⇒ ( η v ⃗ − η ′ d ⃗ ) × n ⃗ = 0 \begin{aligned}
& \eta(\vec v\times \vec n) = \eta'(\vec d\times \vec n) \\
\Rightarrow & (\eta\vec v - \eta'\vec d)\times\vec n = \bf 0
\end{aligned}
⇒ η ( v × n ) = η ′ ( d × n ) ( η v − η ′ d ) × n = 0
这说明 η v ⃗ − η ′ d ⃗ \eta\vec v - \eta'\vec d η v − η ′ d η v ⃗ x = η ′ d ⃗ x \eta\vec v_x = \eta'\vec d_x η v x = η ′ d x v ⃗ x = v ⃗ − ( v ⃗ ⋅ n ⃗ ) n ⃗ \vec v_x = \vec v-(\vec v\cdot\vec n)\vec n v x = v − ( v ⋅ n ) n
d ⃗ x = η η ′ [ v ⃗ − ( v ⃗ ⋅ n ⃗ ) n ⃗ ] d ⃗ y = − n ⃗ 1 − ∣ d ⃗ x ∣ 2 d ⃗ = d ⃗ x + d ⃗ y \begin{aligned}
\vec d_x &= \frac{\eta}{\eta'}[\vec v-(\vec v\cdot\vec n)\vec n] \\
\vec d_y &= -\vec n\sqrt{1-|\vec d_x|^2} \\
\vec d &= \vec d_x + \vec d_y
\end{aligned}
d x d y d = η ′ η [ v − ( v ⋅ n ) n ] = − n 1 − ∣ d x ∣ 2 = d x + d y
于是我们可以计算出折射光线。
但实际上,玻璃还会反射。正常情况下,反射率 R R R 菲涅尔效应 ,这是一个非常恐怖的方程(可以阅读这篇知乎:菲涅尔方程(Fresnel Equation) - 知乎 )。好在我们还有一个神仙,叫 Schlick 近似 ,这使得我们可以用一个多项式函数来近似计算菲涅尔方程。
首先我们需要一个基础反射率 R 0 R_0 R 0 0 0 0
R 0 = ( η − η ′ η + η ′ ) 2 R_0 = \left( \frac{\eta-\eta'}{\eta+\eta'} \right)^2
R 0 = ( η + η ′ η − η ′ ) 2
Schlick 近似的公式是,对于入射角 θ \theta θ
R θ = R 0 + ( 1 − R 0 ) ( 1 − cos θ ) 5 R_\theta = R_0 + (1-R_0)(1-\cos\theta)^5
R θ = R 0 + ( 1 − R 0 ) ( 1 − cos θ ) 5
类似地,我们可能需要毛玻璃的效果,即磨砂玻璃,所以和前面的模糊反射一样,我们设置 f u z z fuzz f u z z
除了实心的玻璃球之外,我们还可以考虑手动实现空心的玻璃球,但这是没必要的。单纯使用两个球体就可以解决:假如定义一个折射率为 η 0 \eta_0 η 0 1 η 0 \frac{1}{\eta_0} η 0 1
下面是玻璃类的实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Glass : public Material { private : Color attenCol; double eta; double R0; double fuzzReflect, fuzzRefract; double getR (const double &cosTheta) const return R0 + (1 - R0) * pow (1 - cosTheta, 5 ); } public : Glass (double _eta = 1.5 , double _fuzzReflect = 0 , double _fuzzRefract = 0 ) : attenCol (1 , 1 , 1 ), eta (_eta), R0 ((_eta - 1 ) * (_eta - 1 ) / (_eta + 1 ) / (_eta + 1 )), fuzzReflect (_fuzzReflect), fuzzRefract (_fuzzRefract) {} Glass (const Color &_attenCol, double _eta = 1.5 , double _fuzzReflect = 0 , double _fuzzRefract = 0 ) : attenCol (_attenCol), eta (_eta), R0 ((_eta - 1 ) * (_eta - 1 ) / (_eta + 1 ) / (_eta + 1 )), fuzzReflect (_fuzzReflect), fuzzRefract (_fuzzRefract) {} bool scatter (const Ray &rayIn, const hitResult &res, Color &atten, Ray &rayOut) const override double realETA = eta; Vec3 realN = res.n; if (dot (rayIn.dir, res.n) > 0 ) { realETA = 1.0 / realETA; realN = -realN; } double cosTheta = dot (-rayIn.dir, realN); double sinTheta = std::sqrt (1 - cosTheta * cosTheta); if (sinTheta * realETA > 1.0 || rnd.rand <double >(0 , 1 ) < getR (cosTheta)) { Vec3 outDir = rayIn.dir - 2 * dot (rayIn.dir, realN) * realN + fuzzReflect * rnd.randUnit (); if (dot (outDir, realN) < 0 ) return false ; rayOut = Ray (rayIn.at (res.t), outDir.unit ()); atten = attenCol; return true ; } Vec3 outX = realETA * (rayIn.dir + realN * cosTheta); Vec3 outY = -realN * std::sqrt (std::fabs (1 - outX.len2 ())); Vec3 outDir = outX + outY + fuzzRefract * rnd.randUnit (); if (dot (outDir, realN) > 0 ) return false ; rayOut = Ray (rayIn.at (res.t), outDir.unit ()); atten = attenCol; return true ; } };
我们在主函数中添加两个玻璃类型的球:
1 2 3 4 5 6 7 8 9 10 11 12 int main () HittaleSet objs; objs.insert (make_shared <Sphere>(make_shared <Diffuse>(Color (0.5 , 0.6 , 0.7 )), Vec3 (0 , 0.1 , -2 ), 0.5 )); objs.insert (make_shared <Sphere>(make_shared <Diffuse>(Color (0.3 , 0.3 , 0.3 )), Vec3 (0 , -100.5 , -2 ), 100 )); objs.insert (make_shared <Sphere>(make_shared <Glossy>(), Vec3 (-1 , 0.5 , -2 ), 0.4 )); objs.insert (make_shared <Sphere>(make_shared <Glossy>(Color (0.9 , 0.5 , 0.3 ), 0.3 ), Vec3 (1 , 0 , -1.5 ), 0.3 )); objs.insert (make_shared <Sphere>(make_shared <Glass>(), Vec3 (0.7 , -0.2 , -1 ), 0.3 )); objs.insert (make_shared <Sphere>(make_shared <Glass>(Color (0.7 , 0.9 , 0.8 ), 1.5 , 0.3 , 0.3 ), Vec3 (-0.5 , -0.1 , -1 ), 0.2 )); Camera cam (16.0 / 9.0 , 800 , 2.0 , 1.0 , Vec3(0 , 0 , 0 ), 50 , 10 ) ; cam.render (objs); return 0 ; }
渲染结果为:
万能的区域类和程序优化
上面的程序跑出来的这个玻璃球看起来挺怪的。尤其是左边的有色玻璃,不管是长相还是颜色。对于长相,像一个鸡蛋,里面一圈深色,外面颜色较浅。对于颜色,实际上,这个颜色是错误的。我们先来考虑简单一点的,即颜色错误的问题。这是因为我们现在的颜色衰减,是根据反射或折射的次数决定的,但现实里,显然是由光线在介质中传播的距离决定的。
为了实现更真实的有色玻璃,我们需要想个办法能计算光线在这个几何体里面走了多远。——而且最好能避免直接把材料类和几何类直接耦合起来,那写死人了。
为了实现这一点,我们写一个额外的区域类。这样就能方便我们实现光线在介质中传播的距离,同时也方便实现后续实现一些“飘渺”的东西,比如体积雾。
区域类负责干的事情是处理光线在体积内的移动距离。当然我们顺便把颜色吸收的系数也可以移植进来,更加方便计算。
对于一个区域,我们希望能记录这个区域的边界(几何类)、材质(材料类)和颜色吸收量。我们希望用光线的路径长度 d i s dis d i s a t t 0 att_0 a t t 0 a t t e n atten a t t e n
a t t e n = e − d i s ⋅ a t t 0 atten = e^{-dis\cdot att_0}
a t t e n = e − d i s ⋅ a t t 0
需要注意的是,这是光线能穿过区域的情况,即区域透明,显然不能用在漫反射和镜面反射材料上。这是很好解决的问题:给每个材料,标记一下是否透明即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class wrapZone : public Hittable { public : shared_ptr<Hittable> bnd; shared_ptr<Material> mat; Color att0; wrapZone (shared_ptr<Hittable> _bnd, shared_ptr<Material> _mat, const Color &_col) : bnd (_bnd), mat (_mat), att0 (_mat->isTrans ? _White - _col : _col) {} bool hit (const Ray &ray, Interval rangeT, hitResult &res) const override return bnd->hit (ray, rangeT, res); } Color atten (const Ray &ray) const { if (!mat->isTrans) return att0; hitResult res1, res2; if (!bnd->hit (ray, Interval (-INFINITY, INFINITY), res1)) return Color (1 , 1 , 1 ); if (!bnd->hit (ray, Interval (res1. t + 0.0001 , INFINITY), res2)) return Color (1 , 1 , 1 ); double dis = res2. t - res1. t; return Color (std::exp (-att0. x * dis), std::exp (-att0. y * dis), std::exp (-att0. z * dis)); } bool scatt (const Ray &rayIn, const hitResult &res, Ray &rayOut) const return mat->scatter (rayIn, res, rayOut); } };
由于我们在这里定义了颜色衰减率 a t t 0 att_0 a t t 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 int main () HittaleSet objs; objs.insert (make_shared <wrapZone>( make_shared <Sphere>(Vec3 (0 , 0.1 , -2 ), 0.5 ), make_shared <Diffuse>(), Color (0.5 , 0.6 , 0.7 ) )); objs.insert (make_shared <wrapZone>( make_shared <Sphere>(Vec3 (0 , -100.5 , -2 ), 100 ), make_shared <Diffuse>(), Color (0.3 , 0.3 , 0.3 ) )); objs.insert (make_shared <wrapZone>( make_shared <Sphere>(Vec3 (-1 , 0.5 , -2 ), 0.4 ), make_shared <Glossy>(), Color (1 , 1 , 1 ) )); objs.insert (make_shared <wrapZone>( make_shared <Sphere>(Vec3 (1 , 0 , -1.5 ), 0.3 ), make_shared <Glossy>(0.3 ), Color (0.9 , 0.5 , 0.3 ) )); objs.insert (make_shared <wrapZone>( make_shared <Sphere>(Vec3 (0.7 , -0.2 , -1 ), 0.3 ), make_shared <Glass>(), Color (1 , 1 , 1 ) )); objs.insert (make_shared <wrapZone>( make_shared <Sphere>(Vec3 (-0.5 , -0.1 , -1 ), 0.2 ), make_shared <Glass>(1.5 , 0.3 , 0.3 ), Color (0.7 , 0.9 , 0.8 ) )); Camera cam (16.0 / 9.0 , 800 , 2.0 , 1.0 , Vec3(0 , 0 , 0 ), 50 , 10 ) ; cam.render (objs); return 0 ; }
HittableSet 中的元素类型,也从父类 Hittable 改成 wrapZone.
最后重构 getRayColor 的逻辑,因为现在颜色吸收不再从材料里读取,而是从区域类里读取。hitResult 中,材料类改为体积类。然后:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 Color getRayColor (const Ray &ray, const HittaleSet &objs, int dep) { if (dep == 0 ) return _Black; hitResult res; if (objs.hit (ray, Interval (0.0001 , INFINITY), res)){ Ray scat; auto obj = res.zone; if (obj->scatt (ray, res, scat)) return obj->atten (ray) * getRayColor (scat, objs, dep - 1 ); return _Black; } double k = 0.5 * (ray.dir.y + 1 ); return (1 - k) * _White + k * Color (0.7 , 0.7 , 1 ); }
下面来考虑鸡蛋的形状。我们修改毛玻璃的逻辑,不要在调整后不符合条件就返回,而是找到一个符合条件的结果返回:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Glass : public Material { private : double eta; double R0; double fuzzReflect, fuzzRefract; double getR (const double &cosTheta) const return R0 + (1 - R0) * pow (1 - cosTheta, 5 ); } public : Glass (double _eta = 1.5 , double _fuzzReflect = 0 , double _fuzzRefract = 0 ) : eta (_eta), R0 ((_eta - 1 ) * (_eta - 1 ) / (_eta + 1 ) / (_eta + 1 )), fuzzReflect (_fuzzReflect), fuzzRefract (_fuzzRefract), Material (true ) {} bool scatter (const Ray &rayIn, const hitResult &res, Ray &rayOut) const override double realETA = eta; Vec3 realN = res.n; if (dot (rayIn.dir, res.n) > 0 ) { realETA = 1.0 / realETA; realN = -realN; } double cosTheta = dot (-rayIn.dir, realN); double sinTheta = std::sqrt (1 - cosTheta * cosTheta); if (sinTheta * realETA > 1.0 || rnd.rand <double >(0 , 1 ) < getR (cosTheta)) { Vec3 outDir = rayIn.dir - 2 * dot (rayIn.dir, realN) * realN + fuzzReflect * rnd.randUnit (); while (dot (outDir, realN) < 0 ) outDir = rayIn.dir - 2 * dot (rayIn.dir, realN) * realN + fuzzReflect * rnd.randUnit (); rayOut = Ray (rayIn.at (res.t), outDir.unit ()); return true ; } Vec3 outX = realETA * (rayIn.dir + realN * cosTheta); Vec3 outY = -realN * std::sqrt (std::fabs (1 - outX.len2 ())); Vec3 outDir = outX + outY + fuzzRefract * rnd.randUnit (); while (dot (outDir, realN) > 0 ) outDir = outX + outY + fuzzRefract * rnd.randUnit (); rayOut = Ray (rayIn.at (res.t) - 0.001 * realN, outDir.unit ()); return true ; } };
运行得到图片:
质量有明显提高。